Physics of Stream/Depth & Rowing

(Part of Physics of Rowing)

Recent Modifications

Contents

  1. Introduction
  2. Viscosity
  3. Boat Resistance
  4. River Flow
  5. Upstream/Downstream Resistance
  6. Shallow Water Resistance
  7. Upstream/Downstream Times

1. Introduction

The creation of this page was prompted by discussions on the rec.sport.rowing newsgroup about why rowing upstream or downstream feels different, and also the difference between deep/shallow water. I'll start by saying I'm assuming that rowing downstream feels 'heavier' than rowing upstream, which is my personal impression although some would argue it's the other way around - which I can't explain except as a purely psychological effect. Also, I'm discounting the change in air resistance, i.e. when you row downstream you're always moving faster relative to the air than rowing upstream, so relatively speaking, downstream pieces are into more of a headwind than upstream pieces. This is clearly correct but, I think, negligible - again speaking personally, I reckon that I can tell the difference between increased water resistance and increased air resistance, and the upstream/downstream difference feels like water resistance to me.

2. Viscosity

Consider two surfaces separated by fluid, a distance H apart, with the upper surface moving at V and the lower surface fixed. The fluid adjacent to the upper surface will be dragged along and also be moving at velocity V while the fluid adjacent to the lower surface will be stationary, so that a constant velocity gradient V/H (also known as 'shear') is set up in the fluid.

Figure (2.1)

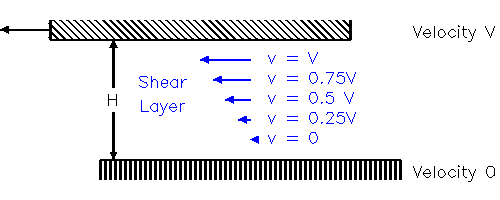
As any physics textbook will tell you, the Resistance R (measured as force per unit area) caused by viscosity is given by:

(2.1) R = e dv/dz

where e is the coefficient of viscosity (measured in kg/m/s, assumed constant), and the shear dv/dz = V/H in this case, so

(2.2) R = e.V/H

This tells you that viscous drag (resistance) on the upper surface increases in proportion to velocity. However, this is only really applies to situations where the horizontal lengths are much larger than the separation H, so that the shear layer is constant along the whole length. This is only true for boats rowing over very shallow (inches) water. For most purposes, a better model is required.

3. Boat Resistance

As a boat moves through stationary water, the water in contact with the bows is immediately accelerated to the boat speed V, but the shear layer can only grow downwards at a fixed speed W (set by the mean free path of molecules). So the lower (static) boundary of the shear layer slopes downwards from the bows:

Figure (3.1)

Below point x along the hull, the boundary layer will have been growing for a time t=x/V, so will have reached a depth h=W.t=W.x/V. So using Eq.(2.1), the viscous drag at point x is given by:

(3.1) R(x) = e.V2/(W.x)

This is the origin of the V2 law for boat resistance (cf. resistance proportional to V in previous section) - see Section 2 of Basics

4. River Flow

River flow is driven by the hydrostatic pressure gradient, which is constant across the whole cross section of the river. Were it not for viscosity effects, this would mean that the stream flowed at an equal speed at all points within the cross-section since each point is driven with the same force. However, due to viscosity, the flow is slower near the fixed boundary (riverbed and banks) and faster near the free boundary (surface, since the air offers relatively little resistance to flow), and the quickest flow will be the furthest from the fixed boundary, which means away from the sides and where the river is deepest.

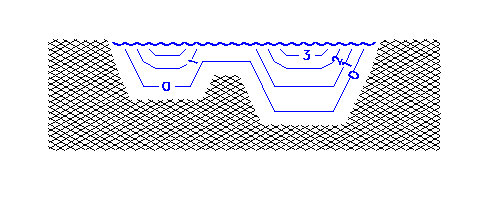
Figure (4.1)

The diagram shows a cross-section of flow over an uneven river bed, the contours represent flow speed. Flow is 0 next to fixed boundary, 1 for 1 layer away, and so on. As with most rivers, being wider than deep, the flow rate in most places is determined by the depth rather than the distance from the sides. The surface flow is therefore quickest (3) over the right hand channel and slowest tucked right in to the sides, or over the central ridge.

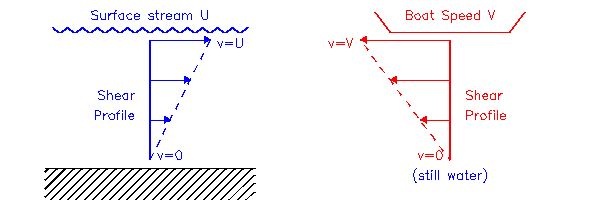
5. Effect of River Flow on Resistance

If there is any flow, the stream will have its own vertical shear (left diagram in Fig. 5.1). From Section 3, a boat moving through still water will also set up its own shear layer at some fixed point beneath the hull (right diagram).

Figure (5.1)

When we have a boat moving in a stream, these two shears will sum as in Fig. (5.2)

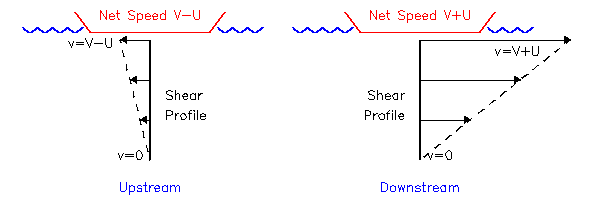
Figure (5.2)

The left diagram shows the shear set up by a boat moving upstream at speed V relative to the water, which is itself moving at speed U relative to the bank or the riverbed. In this case there is some cancellation between the two shear layers: the velocity shear under the boat is reduced so there is less apparent drag compared to the still water case. The right diagram shows the opposite situation for a boat moving downstream. Here the shear and apparent drag are increased.

In general, the faster the flow, or the shallower the water, the greater the shear so the greater the difference in resistance.

6. Shallow Water Resistance

The difference between sections 2 and 3 was that in the former case the shear layer had fixed depth whereas in the latter it grew continuously as the boat passed over.

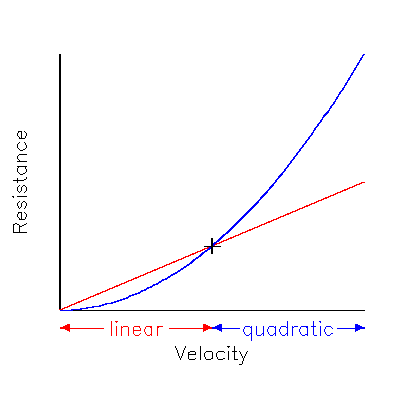
Figure (6.1)

In shallow water, the shear layer may touch the bottom, in which case it obviously ceases to grow and Eq.(2.2) applies instead of Eq.(3.1). At first sight this might seem like a good thing, since in Eq.(2.2) the drag only increases linearly with velocity rather than the square of the velocity from Eq.(3.1). However you have to remember that bottom effects are felt at low velocities rather than high velocities (since the shear layer has more time to grow downwards at low speeds) and the point where the two become equal is where the shear layer separates from the bottom.

So at low velocities the shallow water resistance is linear (shown by the red line in Fig 6.1) and greater than would be expected from the quadratic regime (shown by the blue line) with an unbounded shear layer. Changing the depth of the water has the effect of reducing the slope of the linear regime (differentiating Eq.(2.2)):

(6.1) dR/dV = e/H

so that the transition (at the point + in the diagram) from linear to quadratic occurs at lower velocities.

So how shallow does the water have to be before you notice the bottom? You can get an idea of the depth of the shear layer by observing the extent of the sideways turbulence at the stern of the boat (the shear layer probably grows downwards at much the same rate as outwards), i.e. around 1 metre. Any deeper and you shouldn't notice the bottom at all. The minimum depth for Olympic Regatta courses is, I believe, 2 metres, just to be on the safe side.

Of course, as the speed tends to zero, the shear layer will extend to infinity so the actual depth of the water will always be 'noticed' eventually, but usually at such low resistances that it will be impossible to distinguish between the linear and quadratic regimes.

Note that moving water will also have flowed-induced shear (section 5), an entirely separate effect. In that case (i.e. rivers) the total depth will always be significant.

7. Upstream/Downstream times

It is a common misconception that if you row, say, 2000m upstream, and 2000m downstream, measured against some fixed points on the bank, your average time is the same as if you rowed 2000m in still water (I'm ignoring any change in speed due to fatigue or the effects discussed in the previous sections). For low stream speeds it is a reasonable approximation, but the average in stream will always be slower than your still water time. Why? Because...

Suppose your intrinsic speed through the water is V, the stream speed is U, and you're rowing a distance L measured along the bank.

(7.1) Still water Time, tS = L /V
(7.2) Upstream Time, tU = L /(V-U)
(7.3) Downstream Time, tD = L /(V+U)
(7.4) Average Time, tA = ½(tU +tD) = L.V /(V2- U2)

As you'd expect, as stream speed U tends to zero, then the average of your (upstream+downstream) times tends towards your still water time, but for any non-zero stream, tA is longer than tS (because V2-U2 is always less than V2).

How different? Take V=5 m/s (corresponding to tS=6:40 = 400s, for 2000m in still water). Rowing in a (slowish) stream of U=10 cm/s, you'd row 2000m upstream in tU=408.2s, and downstream in tD=392.2s, giving an average of tA=400.2s, i.e. only 0.2s slower, not important. But in a quicker stream of U=1m/s, you'd get tA=416.7s, i.e. 16.7s out, or you'd think you were about 5 lengths slower than you really are. Note that although the stream speed increased by a factor 10, the error increased by a factor 100 (depends on U2).