RFM Viewing Geometries
Contents
25MAR24

Introduction

The definition of viewing geometry depends on which of three possible representations of the atmosphere are used. In order of increasing complexity these are:
  1. Homogeneous
  2. Plane-parallel (1D)
  3. Circular (2D)

The homogeneous case, suitable for representing lab measurements or horizontal paths in the free atmosphere, is trivial and, apart from temperature, pressure and composition, the only additional parameter required to define the 'view' is the path length. For such cases, usually the only calculation required is of path transmittance.

The plane-parallel representation treats the atmosphere as a set of horizontal layers. The viewing direction is specified by secθ (equivalent to an 'air mass factor'), where θ is the angle with respect to the vertical. Provided that θ represents the viewing angle at the surface rather than the satellite, this generally provides an acceptable simulation for nadir-viewing instruments, at least for secθ≲2 (or θ≲60°)

The circular atmosphere is the most general case, allowing for the curvature of the earth, refraction and field-of-view convolution. The curvature is assumed fixed over the path length, i.e., profile levels forming concentric circles in the viewing plane. Viewing directions can be specified either as tangent heights (for limb-viewing) or elevation angles α relative to the observer horizontal (suitable for geometries which intersect the surface or upward views from within the atmosphere), in which case the observation altitude is also required.

In principle, nadir-views for the circular (α=-90°) and plane-parallel (θ=0°) atmospheres are identical, refraction and curvature having no effect; however small differences arise from the different path integration methods.

When running the RFM, the basic viewing geometry is specified in the driver table by the appropriate flag in the *FLG section and further details in the sixth primary section (labelled *TAN, *GEO, *ELE, *SEC or *LEN)

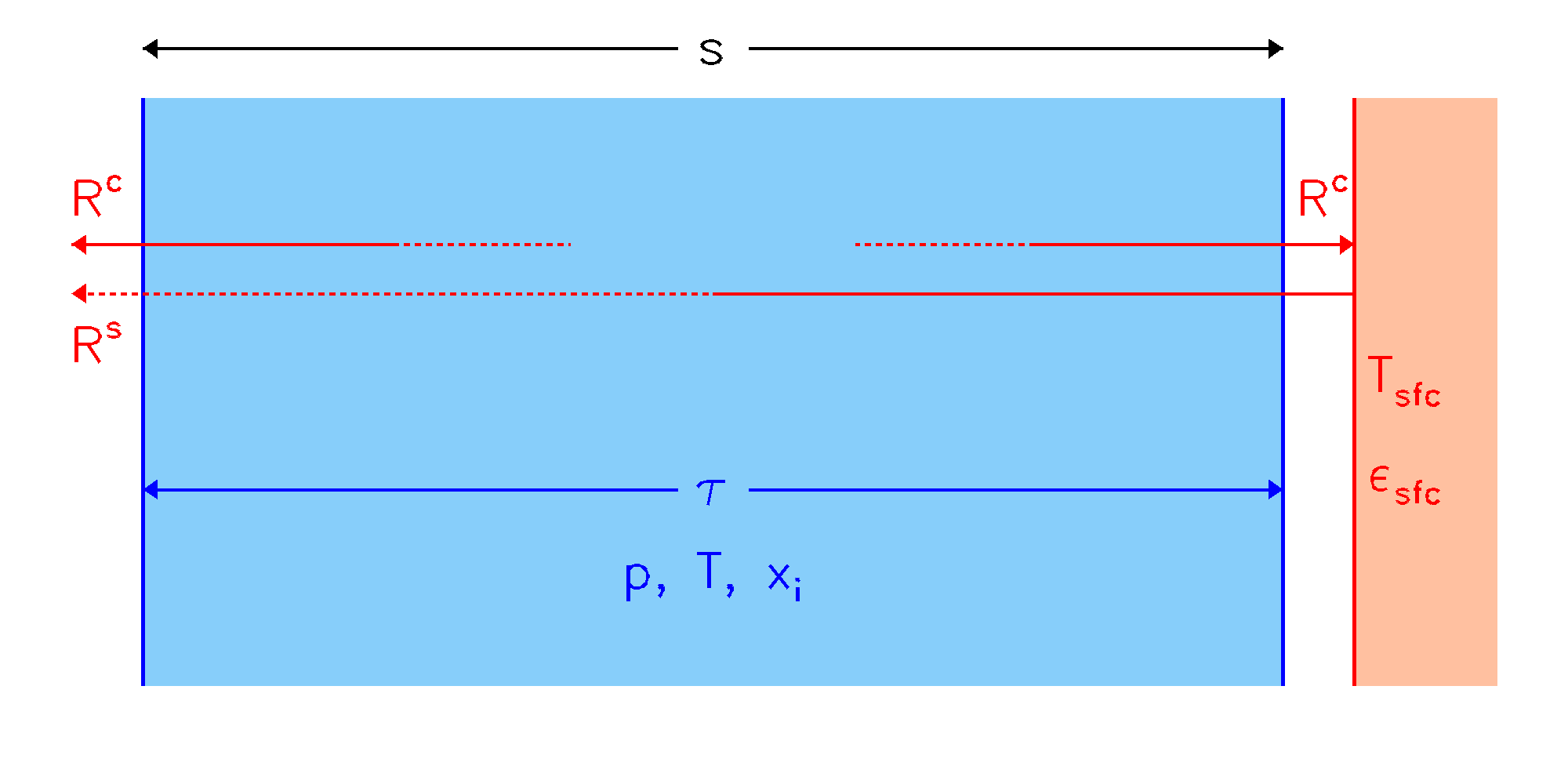
Homogeneous Path

RFM Homogeneous Path Configuration
hom
The user specifies temperature T, pressure p, volume mixing ratios xi of absorbing molecules and a path length s, from which τ, representing transmittance, absorption or optical depth is calculated. A radiance R can also be calculated (left of plot) which will be the sum of the cell emission Rc and the attenuated emission Rs of a background surface of temperature Tsfc. For surface emissivity εsfc < 1, Rs will also include a reflected component of Rc.
For homogeneous path calculations it is necessary to specify the following in the driver table.
*FLG section
Add HOM flag, which tells the RFM that there is a single path segment to be modelled.
*TAN (or *LEN) section
Length of path, in km. In fact multiple path lengths can be calculated at the same time, although I doubt you will need this feature. The path length is specified in km by default (for consistency with the units used in the tangent height definition for limb-viewing), but you can also specify alternative units, eg UNITS=CM.
The 'atmosphere' (i.e., temperature, pressure and composition) for a homogeneous path is specified in the *ATM section of the driver table, either using a single 'profile level' .atm file, and/or directly within the *ATM section itself using a series of PARAMETER=VALUE pairs, e.g. TEM=296, CO2=400

It is assumed that most homogeneous path calculations will be for transmittance but radiance can also be calculated. Then it is necessary to consider the boundary condition at the remote end of the path. By default, the RFM assumes a space view, but by using the SFC flag and *SFC section, any boundary temperature and emissivity can be specified.

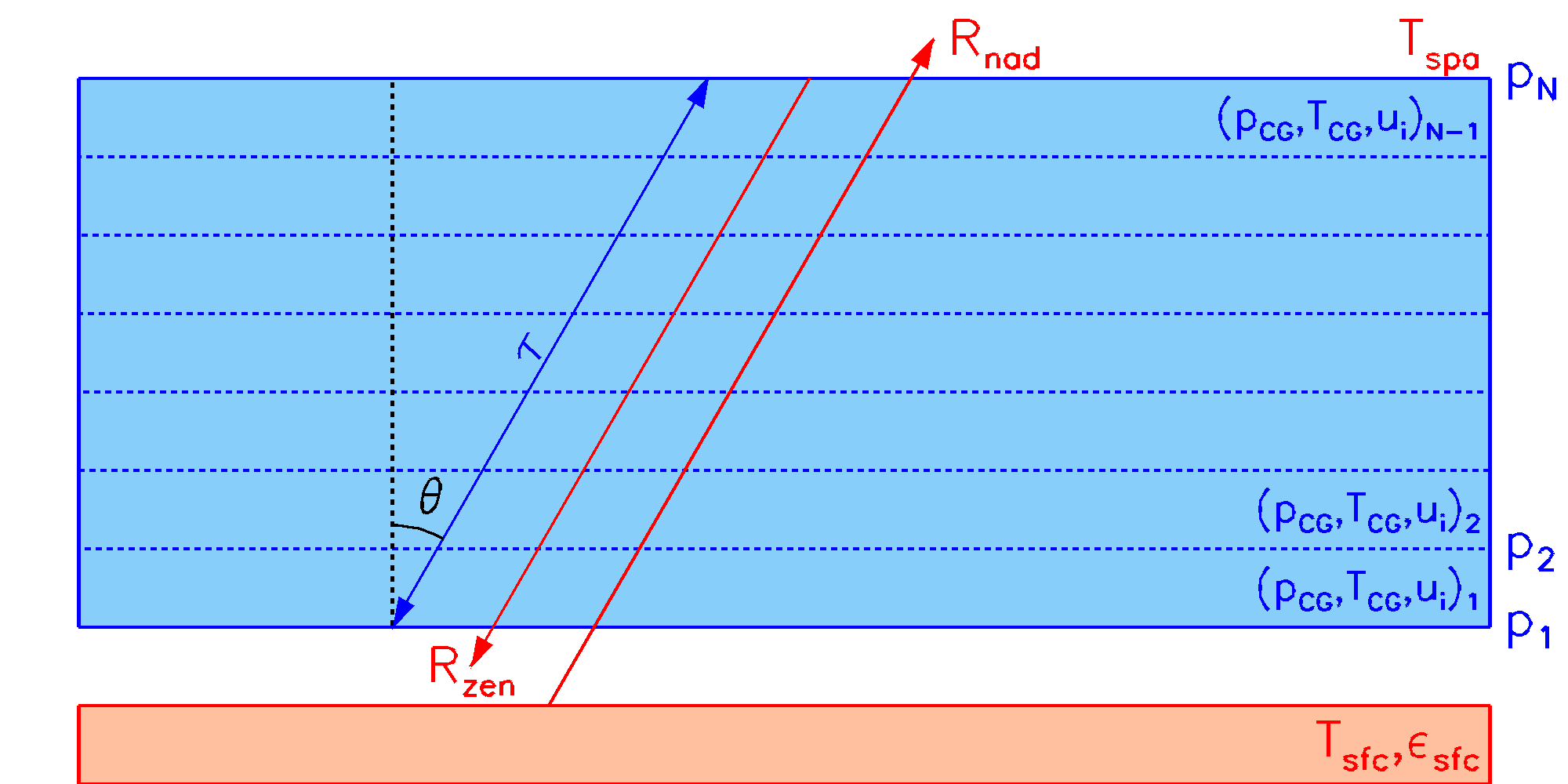
Plane Parallel

RFM Plane Parallel Configuration
planar

The user selects either a Zenith or a Nadir view and specifies an air-mass factor secθ, where θ is the angle of the path to the vertical (secθ=1 for a vertical path).

The user specifies atmospheric profiles of temperature Tj and volume mixing ratios xi,j of absorbing molecules at N pressure levels pj. From this the RFM defines N-1 layers, each characterised by Curtis-Godson equivalent parameters TCG, pCG and partial columns ui.

The upward-looking radiance (at the surface) Rzen is initialised with the space background radiance Tspa (usually negligible except for microwave region). The downward-looking radiance (from space) Rnad, for a non-reflective surface is initialised with the surface emission. Both calculations then proceed though the atmosphere treating each layer as a homogeneous path. (For a reflective surface there is first a downward radiance calculation, of which a reflected component is added to the surface emission.)

Atmospheric transmittance, absorption or optical depth, represented by τ, is the same for both nadir and zenith directions.

The plane parallel assumption treats the atmosphere as a series of horizontally-uniform layers, and the viewing geometry is simply defined by the (constant) angle of the ray-path with respect to the vertical.

An advantage of this assumption is that Curtis-Godson equivalent paths can be calculated analytically from the atmospheric profile values, and (for any given absorber) CG mean pressure and temperature are independent of viewing angle.

In principle effects such as refraction and field-of-view convolution could be applied to such an atmosphere, but the RFM only applies these for the circular geometry.

For basic ray calculations through a plane-parallel atmosphere it is necessary to specify the following in the driver table

*FLG
Either ZEN (upward viewing) or NAD (downward viewing) flags.
*TAN (or *SEC section)
secθ value of path(s), where θ is the angle to the vertical. Thus only values secθ ≥ 1 are allowed and secθ=1 specifies a vertical path.
If nadir-viewing (NAD flag), then the surface flag (SFC) is also required. The RFM assumes, by default, that the surface has an emissivity of 1 (i.e., blackbody) and a temperature equal to the temperature at the base of the atmosphere. These values may be altered using the *SFC section of the driver table.

If an observer altitude is specified within the atmosphere (OBS flag) then the viewing geometry may alternatively be specified by an elevation angle α, in degrees, relative to the horizontal. This is done by replacing the section label *TAN (or *SEC) with *ELE. The RFM accepts values of 0.1 ≤ |α| ≤ 90.0, where α=90 corresponds to viewing vertically upward.

Flux calculations (FLX Flag), which involve integration over solid angle, also use the plane-parallel assumption.

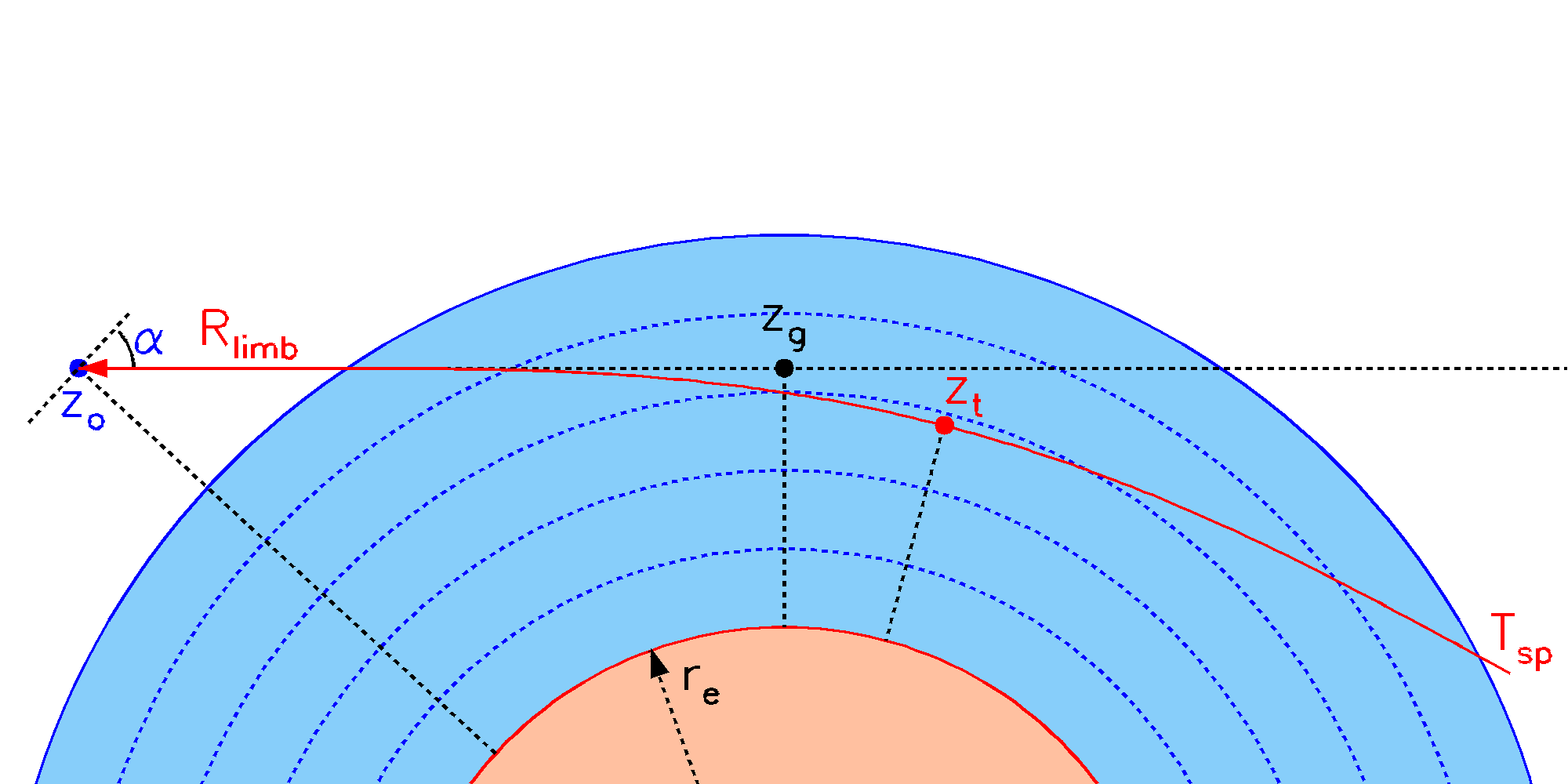
Circular Geometry

RFM Limb-Viewing Configuration
limb

The ray-path, shown in red can be specified in three ways:

  1. By the refracted tangent height zt
  2. By the geometric (or projected) tangent height zg
  3. By elevation angle α, which also requires the observation altitude zo
Altitudes are defined (z=0) relative to the radius of curvature re.

The atmosphere is defined in the same way as the plane parallel atmosphere, although in this case the Curtis-Godson equivalent parameters are derived for each path separately.

The default option (ie in the absence of HOM, NAD, ZEN or FLX flags) is for viewing a circular atmosphere. This includes refraction and allows for field-of-view convolution. It is necessary to include an altitude profile in the *ATM section of the driver file since this is required to establish the local curvature of the atmosphere for ray-tracing.

The ray path is specified according to how the *TAN section of the driver file is labelled.

*TAN (usual case)
Path specified by refracted, or actual, tangent height [km]
*GEO
Path specified by geometric, or projected tangent height [km]. That is: the tangent height that would be expected in the absence of any refraction effects
*ELE
Path specified by elevation angle [deg] above horizontal from the observer. Viewing from above the atmosphere (ie satellites) this would be a negative number. This also requires the observer altitude to be set (OBS flag and *OBS Section).
The radius of curvature for the atmosphere is defined for the altitude 0 km (the actual surface can be at any altitude). By default this is set to a typical earth value (6367.421 km, in phyadj_dat.f90), but can be altered using the RADCRV parameter in the *PHY section of the driver file.